Die symbolischen Eigenfunktionen einer eingespannten dreieckigen Membran ermitteln

Spezifizieren Sie einen Laplace-Operator.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x, y], {x, y}];

Spezifieren Sie homogene Dirichlet-Randbedingungen.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x, y] == 0, True];

Ermitteln Sie die vier kleinsten Eigenwerte und Eigenfunktionen des Operators in einem Dreieck.

In[3]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x, y], {x, y} \[Element] Triangle[], 4];

In[4]:=

vals

Out[4]=

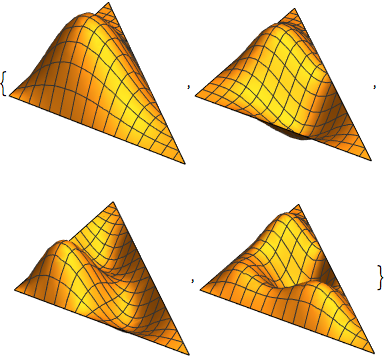
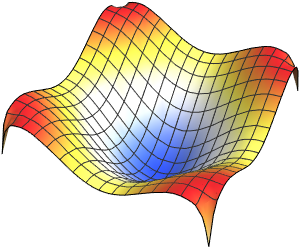
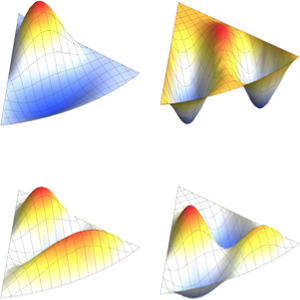
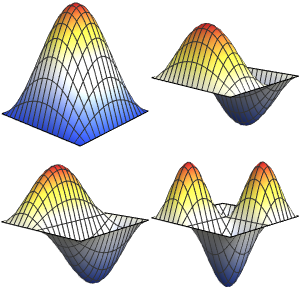
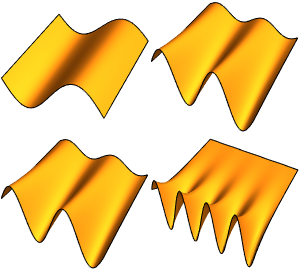
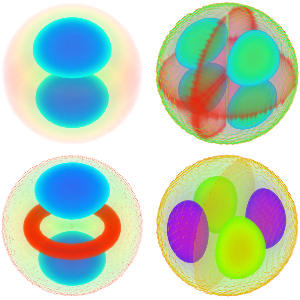
Visualisieren Sie die Eigenfunktionen.

In[5]:=

Table[Plot3D[funs[[i]], {x, y} \[Element] Triangle[], Boxed -> False, Axes -> False, Method -> {"ShrinkWrap" -> True}], {i, 4}]

Out[5]=