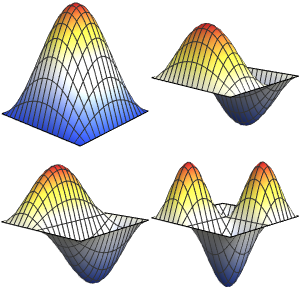
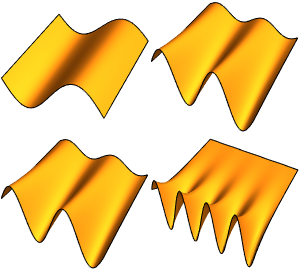
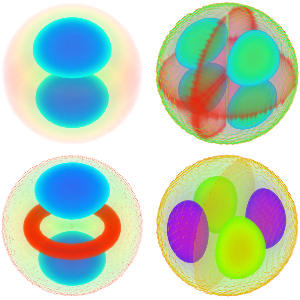
Symbolische Eigenwerte berechnen

Spezifizieren Sie einen 1D-Laplace-Operator.

In[1]:=

\[ScriptCapitalL] = -Laplacian[u[x], {x}];

Spezifizieren Sie eine homogene Dirichlet-Randbedingung.

In[2]:=

\[ScriptCapitalB] = DirichletCondition[u[x] == 0, True];

Ermitteln Sie Ausdrücke für die 5 kleinsten Eigenwerte auf dem Intervall .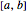

In[3]:=

DEigenvalues[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, a, b}, 5]

Out[3]=

Spezifizieren Sie einen Airy-Operator.

In[4]:=

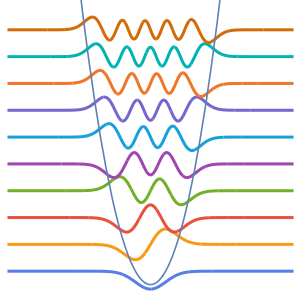
\[ScriptCapitalL] = -Laplacian[u[x], {x}] + x u[x];

Ermitteln Sie die 5 kleinsten Eigenwerte und die entsprechenden Eigenfunktionen.

In[5]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[x], {x, 0, 1}, 5];

Die Eigenwerte sind Wurzeln einer transzendente Gleichung.

In[6]:=

vals[[1]] // TraditionalForm

Out[6]//TraditionalForm=

Berechnen sie einen transzendenten Eigenwert mit hoher Präzision.

In[7]:=

N[vals[[1]], 500] // TraditionalForm

Out[7]//TraditionalForm=

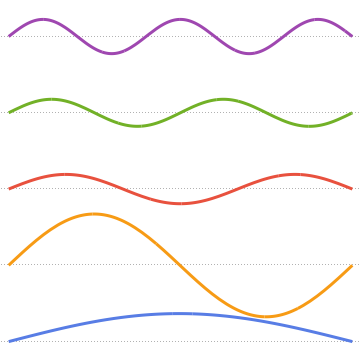
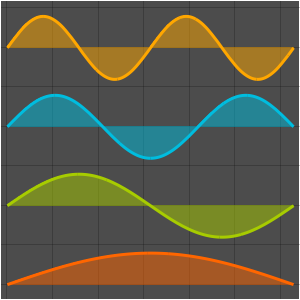
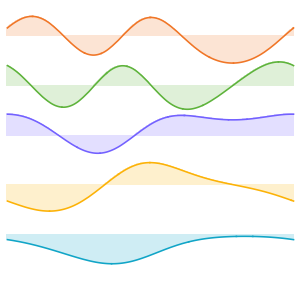
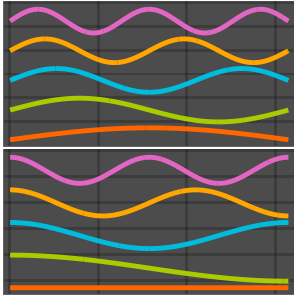
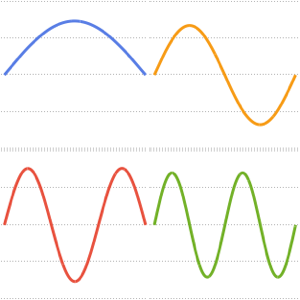
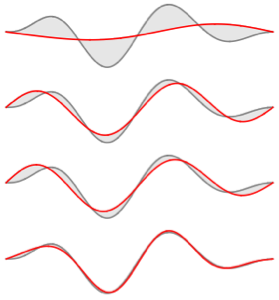
Visualisieren Sie die Eigenfunktionen.

In[8]:=

Plot[Evaluate[funs + Range[5]], {x, 0, 1}, ImageSize -> Medium, PlotTheme -> {"Business", "Bare"}, AspectRatio -> 1]

Out[8]=