Die exakten Eigenmodi der Wärmeleitungsgleichung berechnen

Spezifizieren Sie eine Wärmeleitungsgleichung mit homogenen Dirichlet-Randbedingungen.

In[1]:=

{\[ScriptCapitalL], \[ScriptCapitalB]} = {D[u[t, x], t] == Laplacian[u[t, x], {x}], DirichletCondition[u[t, x] == 0, True]};

Ermitteln Sie die vier kleinsten Eigenwerte und Eigenfunktionen.

In[2]:=

{vals, funs} = DEigensystem[{\[ScriptCapitalL], \[ScriptCapitalB]}, u[t, x], t, {x, 0, \[Pi]}, 4]

Out[2]=

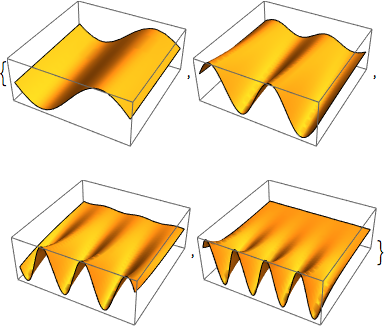
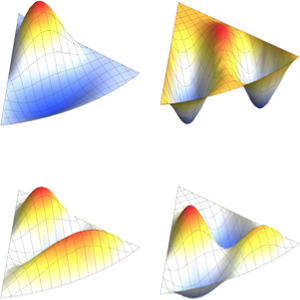
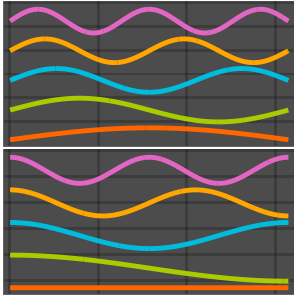
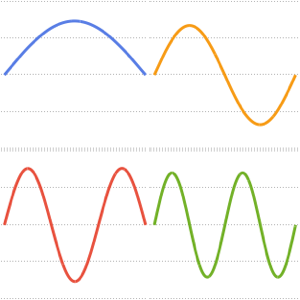
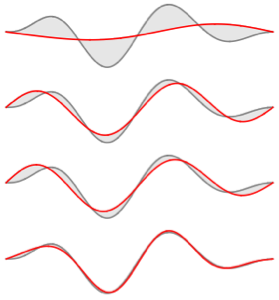
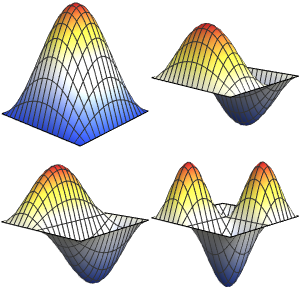
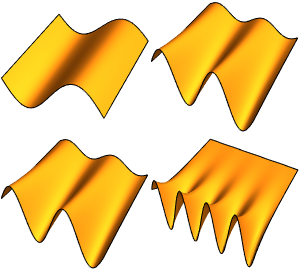
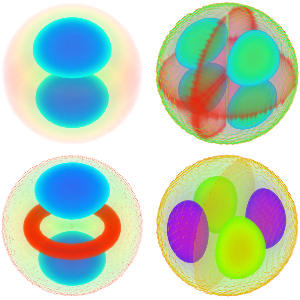
Visualisieren Sie die Eigenfunktionen.

In[3]:=

Table[Plot3D[funs[[i]] // Evaluate, {x, -3, 3}, {t, 0, 1/3}, PlotRange -> All, Ticks -> False, Mesh -> False], {i, 4}]

Out[3]=